Strehl ratio

The Strehl ratio, named after the German physicist and mathematician Karl Strehl (1864-1940), is a measure for the optical quality of telescopes and other imaging instruments. It is defined as the ratio of the observed peak intensity at the detection plane from a point source as compared to the theoretical maximum peak intensity of a perfect imaging system working at the diffraction limit.[1] This is closely related to the sharpness criteria for optics defined by Karl Strehl.[2][3] It can be expressed as 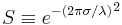S \equiv {e^{-(2\pi\sigma/\lambda)}}^2 with sigma (σ) being the root mean square deviation of the wavefront and lambda (λ) being the wavelength.[4] Unless stated otherwise, the Strehl ratio is usually calculated at the best focus of the imaging system under study.

Usage

The ratio is commonly used to assess the quality of astronomical seeing in the presence of atmospheric turbulence and assess the performance of any adaptive optical correction system. It is also used for the selection of short exposure images in the lucky imaging method.

In industry the Strehl ratio has become a popular way to summarize the performance of an optical design because it gives the performance of a real system, of finite cost and complexity, relative to a theoretically perfect system which would be infinitely expensive and complex to build and would still have a finite point spread function. It provides a simple method to decide whether a system with a Strehl ratio of, for example, 0.95 is good enough, or whether twice as much should be spent to try to get a Strehl ratio of perhaps 0.97 or 0.98.

Further explanation

Visually, diffraction of light is imperfect, even in a perfect optical system. This leads to an observable point spreading phenomenon which produces the so-called Airy disk or disk of light when point sources such as distant stars are magnified. The intensity distribution in the image plane of a point source is generally called the point spread function. The Strehl ratio compares the differences between theoretically perfect point spread and the actual point spread of a given optical device.

Limitations

Characterizing the form of the point-spread function by a single number, as the Strehl Ratio does, will be meaningful and sensible only if the point-spread function is little distorted from its ideal (aberration-free) form, which will be true of a well-corrected system that operates close to the diffraction limit. That includes most telescopes and microscopes, but excludes most photographic systems, for example. The Strehl ratio has been linked via the work of Marechal to an aberration tolerancing theory which is very useful to designers of well-corrected optical systems, allowing a meaningful link between the aberrations of geometrical optics and the diffraction theory of physical optics. A significant shortcoming of the Strehl ratio as a method of image assessment is that, although it is relatively easy to calculate for an optical design prescription on paper, it is normally difficult to measure for a real optical system, not least because the theoretical maximum peak intensity is not readily available.

See also

References

  1. ^ Sacek, Vladimir (July 14), "6.5. Strehl ratio", Notes on amateur telescope optics, http://www.telescope-optics.net/Strehl.htm, retrieved March 2, 2011 
  2. ^ Strehl, K. 1895, Aplanatische und fehlerhafte Abbildung im Fernrohr, Zeitschrift für Instrumentenkunde 15 (Oct.), 362-370.
  3. ^ Strehl, K. 1902, Über Luftschlieren und Zonenfehler, Zeitschrift für Instrumentenkunde, 22 (July), 213-217.
  4. ^ http://www.wolframalpha.com/entities/calculators/Strehl_ratio_formula/av/uo/vo/ Strehl ratio formula

External links